As I work towards a Master’s in applied statistics, my focus is on how these mathematical topics can be applied to real-world situations. In my current Calculus II course, I created Python functions to simplify the tedious calculations involved in Euler’s method, Newton’s law of cooling, sequences, and series.
The final product is a Jupyter Notebook. The project is located in my GitHub repository and available for download.
First-order differential equations
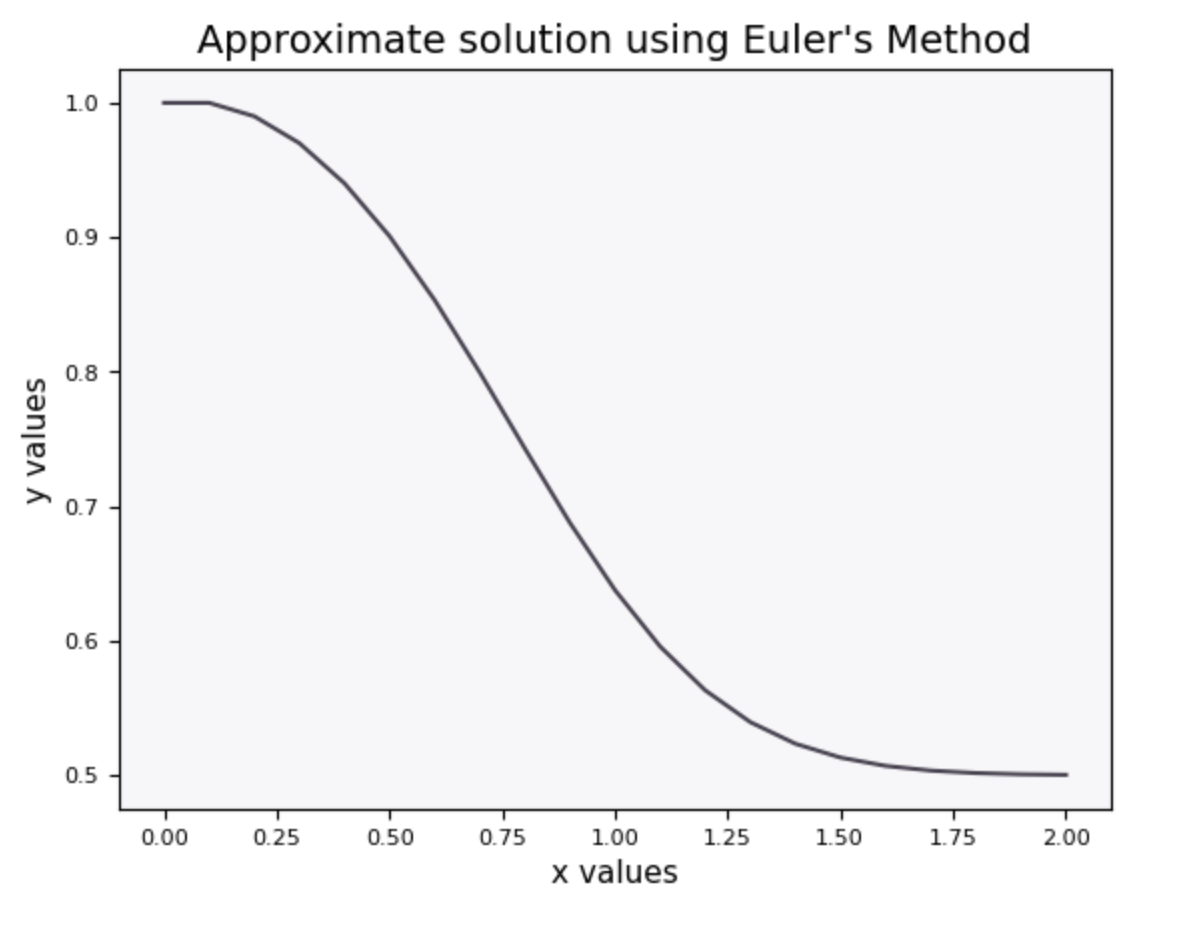
The first section of the Calculus Calculator contains a function to create an approximate solution for a first-order differential equation using Euler’s method.
Euler’s method is used to analyze circuit performance, determine reactivity in chemical reactions, understand bacterial growth, forecast financial systems, and more. If you have installed landscape lights, you will see tables showing the maximum distance you can run a wire before the furthest lights dim. These values came from Euler’s theories.
An additional bonus section includes a function for Newton’s law of cooling.
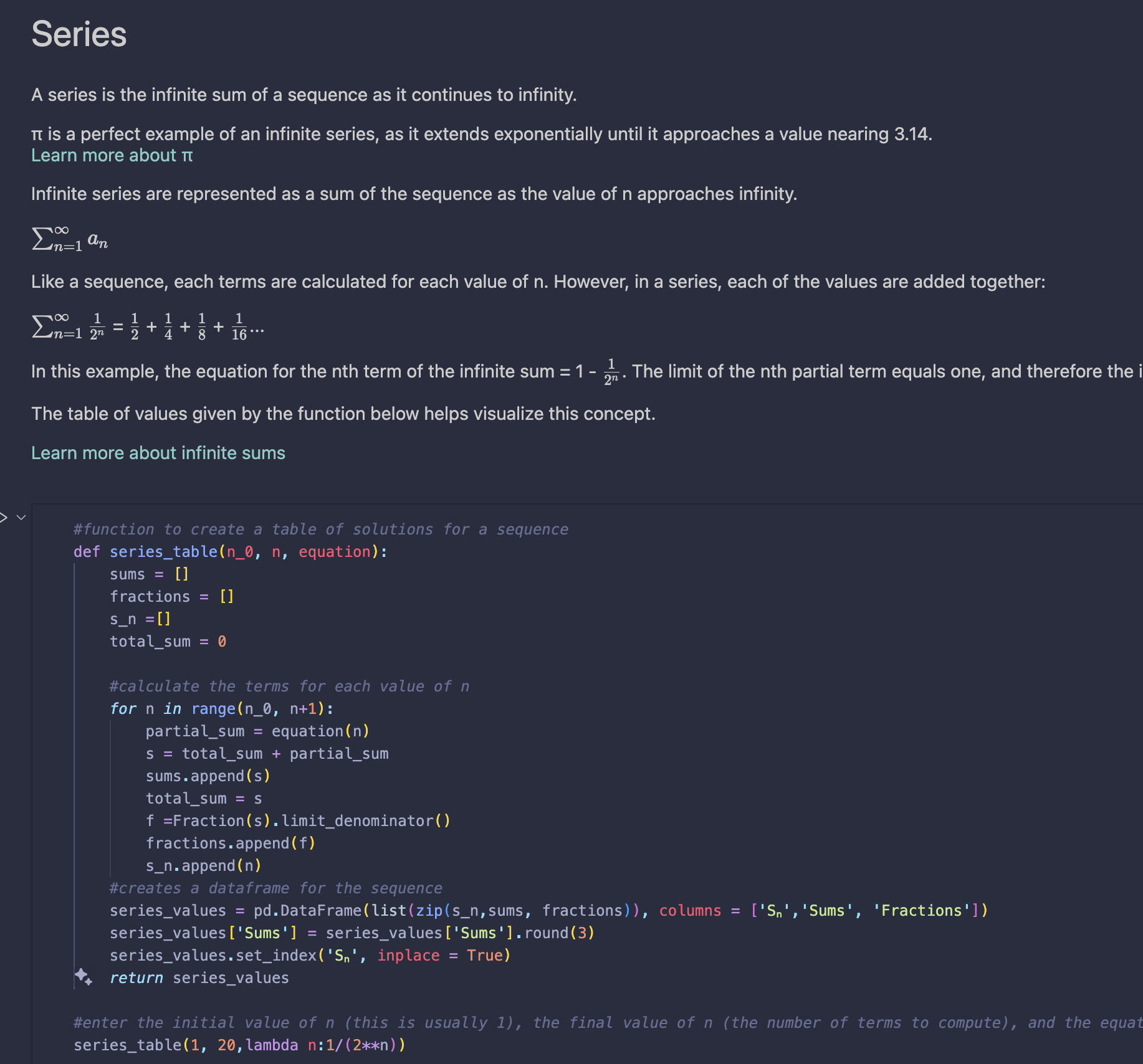
Sequences & Series
Series and sequences represent mathematical equations that are impossible to express in traditional algebraic terms. Binary code, pi, and countless biological systems, such as DNA, are based on sequence.
Documentation
The Jupyter Notebook includes thorough documentation of each Python function and links to additional resources. Enjoy my application of Calculus II.
